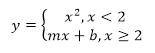Good Problems

These are problems selected from a variety of resources. Whenever possible I will list the source from which it came. There will be no solutions provided here, but if you follow the link to the source there may be solutions there.

Kite Fold #1

For what dimension paper will these folds produce a kite?

Duelling Dice

Consider the following four dice and the numbers on their faces:

• Red : 0, 1, 7, 8, 8, 9
• Blue: 5, 5, 6, 6, 7, 7
• Green: 1, 2, 3, 9, 10, 11
• Black: 3, 4, 4, 5, 11, 12

These are used to play a game for two people. Player 1 chooses one of the die to use for the game. Then player 2 chooses a die. Now each player rolls their die. The player with the highest number showing gets a point. The first player to 7 points wins the game. If you are player 1 which die should you choose. If you are player 2 which die should you choose? [from the Mathematics Task Centre]

Arithmetic Series

Find the sum of the arithmetic series 13 + … + 61.

Lost Primes

Three cards (see below) each have a prime number on the back. The sum of the number on the front and back of each card is the same as the other cards. What are the numbers on the back of each card?

Scrambled Dice

Imagine a typical 6-sided die, and notice that the sum of opposite faces is always seven. The one is across from the six, the two is across from the five, and so on. Now imagine that you were making your own six-sided die that did not have this restriction. How many different dice could be made?

Painted Cube

Paint all the sides of a 3 x 3 x 3 cube. Once it is dry take it apart into its 1 x 1 x 1 unit cubes. How many of these unit cubes have paint on three faces? Two faces? One face? No faces? Explore for 4 x 4 x 4, etc.

Differentiable Function

Consider the differentiable function below. What are m and b?

Puck Play

Ferin and Ian play a game by alternately moving a hockey puck on a board with n concentric circles divided into r regions. For example, in the diagram below, we have n= 4 and r = 8. 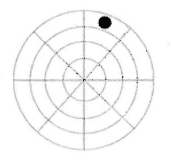The game starts with the puck already on the board, as shown. A player may move either clockwise one position or one position towards the centre, but cannot move to a position that has been previously occupied. The last person who is able to move wins the game. Ferin moves first. Can Ferrin win? Explore. [from Richard Hoshino]

Egg timer

How do you make a 9 minute egg if all you have is a 4 minute and 7 minute egg timer?

Rubic’s Cubeish

You have 27 small cubes, 3 each of nine colours. Use the small cubes to make a 3 by 3 by 3 cube so that each face of the bigger cube contains one of every colour. [from nRICH]

Square Peg in a Round Hole

What is a better fit, a square peg in a round hole or a round peg in a square hole?

Chessboard

How many squares on a chessboard? How many rectangles?

The Last Number

Consider the string 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. Cross out any two numbers in this list and add the difference to the end of the list. This new number is now part of the list. Continue the process of crossing out two number on the list and adding the difference until there remains only one number. What can you say about the last number? Explore. [from Richard Hoshino]

The Desk Calendar

On the desk calendar below, what numbers have to be where in order for every date from 01 to 31 to be able to be represented?

The Pirates and the Diamond 

A band of 10 pirates are going to disband. They have divided up all of their gold, but there remains one GIANT diamond that cannot be divided. To decide who gets it the captain puts all of the pirates (including himself) in a circle. Then he points at one person to begin. This person steps out of the circle, takes his gold, and leaves. The person on his left stays in the circle, but the next person steps out. This continues with every second pirate leaving until there is only one left. Who should the captain point at if he wants to make sure he gets to keep the diamond for himself? What if there were 11 pirates? What if there were 12 pirates?What if there were 27 pirates? Etc.

Honeybee Ancestors

Honeybees have a very interesting genealogy. While female honeybees come from a fertilized egg, male honeybees come from an unfertilized egg. That is, female honeybees have a mother and a father, while male honeybees have only a mother. Look at the family tree of a male honeybee. How many ancestors are there in the previous generation? The one before that? The one before that? How many ancestors 10 generations ago? Etc.

Crossing the Bridge

Adam, Bob, Clair and Dave are out walking: They come to rickety old wooden bridge. The bridge is weak and only able to carry the weight of two of them at a time. Because they are in a rush and the light is fading they must cross in the minimum time possible and must carry a torch (flashlight,) on each crossing.
They only have one torch and it can’t be thrown. Because of their different fitness levels and some minor injuries they can all cross at different speeds. Adam can cross in 1 minute, Bob in 2 minutes, Clair in 5 minutes and Dave in 10 minutes.
Adam, the brains of the group thinks for a moment and declares that the crossing can be completed in 17 minutes. There is no trick. How is this done? [from Nigel Coldwell]

Triangle Perimeter

Determine the minimum perimeter of a triangle with one vertex at (7,1), one vertex on the x-axis, and one vertex on the line y = x. [from Richard Hoshino]

Intersecting Sets

Place 17 objects into the two circles below so that each circle has the same number of objects. How many ways can you do it?

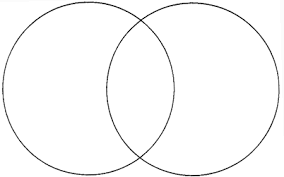
What if you want the ratio of objects in one circle to the other circle to be 4:3 or 12:9?

1001 Pennies

There are 1001 pennies lined up on a table. I come along and replace every second coin with a nickel. Then I replace every third coin with a dime. Finally, I replace every fourth coin with a quarter. How much money is on the table?

Frame the Cards

Arrange ten playing cards (ace to ten) in a rectangle with three cards on two sides and four cards on two sides such that the sum of the cards on every side add up to the same total. [from Annette Rouleau]

Palindromes

Consider the number 28. It is not a palindrome. So, I reverse the number and add it to itself (28 + 82 = 110). 110 is not a palindrome. So, I reverse it and add it to itself (110 + 011 = 121). 121 is a palindrome. This means that 28 is a depth 2 palindrome (it took two iterations to make it a palindrome).  What is the depth of all two digit numbers?

Dart Board Probabilities

Two darts are thrown at a circular target. Where does the first dart have to land so that the probability that the second dart will be closer to the centre is 50%?

Canada Day

On Canada Day Alex stacks dice on top of each other until the sum of the visible faces are equal to the year. When will he next be able to do this? Generalize.

10 Prisoner Release

A warden has decided that his jail is too full, so he wants to release some of the prisoners. His strategy for doing this is that he will take ten prisoners at random and line them up in a row so that each prisoner can only see the prisoners in front of them. The warden will then place a black or white hat on the head of each prisoner. Starting at the back of the row the warden will then ask that prisoner what colour his hat is. If he guesses correctly then he is released. The warden then goes to the next prisoner in line, and so on. The ten prisoners are allowed to meet to discuss before they line up. If they are clever they will come up with a strategy that will guarantee to save some of them. How many could you save?

Fantastic Four

Make the numbers from 1 to 30 using four 4’s and any operations.

Seed Numbers

Consider two whole numbers (for example 3 & 6). These will be the first two numbers. The third number is the sum of the first two (9). The forth is the sum of the previous two (15), and so on (3, 6, 9, 15, 24, 39, …). What do the first two number have to be such that the fifth number is 100?

Bucky the Badger

Bucky the Badger is a mascot for his schools football team. Every time his team scores Bucky does a number of push-ups equal to his team’s total points at that time. If his team finished with 50 points, how many push-ups could Bucky have done? [from Dan Meyer].

Gopher Hunt

Imagine a series of equally spaced holes running along a line infinitely in both directions. A groundhog is in one of the holes and every minute he jumps to a new hole that is some fixed interval of holes away from his current hole. You do not know where he starts, or the interval that he jumps, or the direction that he goes in, but after each of his moves you can shine a flashlight into one (and only one) hole. The problem is to find a method by which you can guarantee to eventually find the groundhog.

Sum of 51

How many 6 digit numbers are there whose digits sum to 51? [from Practice Fermat Number 4, #7]

Concave Polygons

We know that the sum of exterior angles of any convex polygon is 360º. But what if the polygon is concave? What adjustments or extension to the ‘rule’ must be made in order for the sum to still be 360º? [from Robert McGregor on the AAMT]

Gold Chain Extended

You are backpacking through Europe. You have one month left until your flight home, but you have run out of money. However, you have a 50 link gold chain and you have found a hotel that is willing to accept one link per night for payment of room and board. However, the manager wants payment every day and he is willing to help you out by cutting links for you. The problem is that he wants one gold link payment for every link he cuts. What is the most number of links that you will have left when you fly home? [my extension of TestFunda vol. 1 (p. 1)]

105

In how many ways can 105 be expressed as the sum of at least two consecutive positive integers? [from the Canadian Team Math Contest, 2014, #12]

Tax Man

Tax Man is played like this: Start with a collection of paychecks, from $1 to $12. You can choose any paycheck to keep. Once you choose, the tax collector gets all paychecks remaining that are factors of the number you chose. The tax collector must receive payment after every move. If you have no moves that give the tax collector a paycheck, then the game is over and the tax collector gets all the remaining paychecks. The goal is to beat the tax collector.

Example:
Turn 1: Take $8. The tax collector gets $1, $2 and $4.
Turn 2: Take $12. The tax collector gets $3 and $6 (the other factors have already been taken).
Turn 3: Take $10. The tax collector gets $5.

You have no more legal moves, so the game is over, and the tax collector gets $7, $9 and $11, the remaining paychecks.

Total Scores:
You: $8 + $12 + $10 = $30.
Tax Collector: $1 + $2 + $3 + $4 + $5 + $6 + $7 + $9 + $11 = $48.

Questions:
Is it possible to beat the tax collector in this $12 game? If so, how? What is the maximum score you can get?
Bonus: What if you played the game with paychecks from $1 to $24? How about $1 to $48? [from Numberplay, April 13]

Cereal Prizes

Suppose there was one of six prizes inside your favorite box of cereal. Perhaps it’s a pen, a plastic movie character, or a picture card. How many boxes of cereal would you expect to have to buy, to get all six prizes? [from George Reese]

Four Aces

Figure out the Four Aces card trick. [from Peter Liljedahl]

Burning Rope

You have two ropes, each of which takes two hours to burn if lit at one end. These ropes are not homogeneous and some parts of the ropes burn quicker than others. Can you use the ropes to time out 1 hour and 30 minutes? 45 minutes? What other times could you get? [from TestFunda, book 1, #7]

How Many 7’s

If you write out the numbers from 1 to 1000, how many times will you write the number 7?

Marching Band

Students in a marching band want to line up for their performance. The problem is that when they line up in 2’s there is 1 left over. When they line up in 3’s there are 2 left over. When they line up in 4’s there are 3 left over. When they line up in 5’s there are 4 left over. When they line up in 6’s there are 5 left over. When they line up in 7’s there are no students left over. How many students are there? [from John Grant McLoughlin]

Tire Tracks

“This track, as you perceive, was made by a rider who was going from the direction of the school.” observed Sherlock Holmes.
“Or towards it?”, said Watson.
“No, no my dear Watson… It was undoubtedly heading away from the school.”

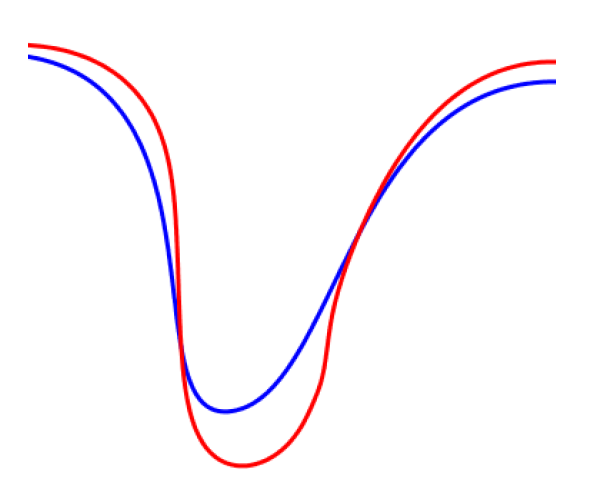
Which way was the bike travelling? [from Jamie Mulholland – presentation at CMEF 2014].

Pirate Hats

Once there was a group of pirates headed by Captain Francis Verney. One night Francis got a question that who among the group would be smart enough to lead the group after he steps down.

So he decided to conduct series of tests, to find the most smart one. As we all know testing the intelligence of pirates is not that simple, as they are clever and rational in nature.

Francis picks up 9 hats, a mix of white hats and black hats. He placed the hats on 9 pirates head and mentioned them that they should not talk and there is at least 1 white hat and black hats count is more than white hats.

Obviously they can’t see their own hat but they can see the color of other 8 hats. If they guess wrong, their head will be blown. Francis gave them 20 mins time to figure out, but no one could.

So he gave another 10 mins. But still everyone kept quite. Finally he gave them 5 mins, and at the end all 9 knows their hat color, and all answered same time. Think about the logic that pirates used to figure out. [from |V|UR@|_I’S BLOG - June 17, 2013]

Black and White Marbles

We place in a box thirteen white marbles and fifteen black. We also have twenty-eight black marbles outside the box. We remove two marbles from the box. If they have a different colour we put the white one back in the box. If they have the same colour we put a black marble in the box. We continue doing this until only one marble is left in the box. What is its colour? [from Vector 55(1) – p. 49]

Tangent Polygons

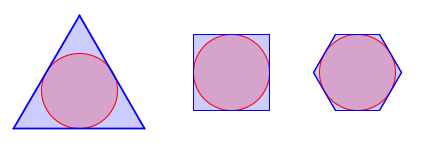
In the diagram various regular polygons, P, have been drawn whose sides are tangents to a circle, C. Show that for any regular polygon drawn in this way:

100 Divided

When 100 is divided by a positive integer x, the remainder is 10.
When 1000 is divided by x, what will the remainder be? [from University of Waterloo CECM Past Contest Archive (2011 Caley, #18)]

Three Jugs

Three jugs have the capacity for 8, 5 and 3 litres respectively. The 8 litre jug is filled entirely with water and the other two jugs are empty. Your task is, by decanting, to divide the water into two equal parts, that is, 4 litres in jug A and 4 litres in jug B, leaving the smallest jug empty. [from MathXTC – Neurological Nasties (problem set 9, #3)]

Escaped Prisoner

Gold Chain

A wealthy man needed to pay the mason building his house. He was running low on cash so he decided to pay the mason with a gold chain made of 7 links. The mason’s fee was equal to one gold link each day. The wealthy man needed to pay the mason each day or he would stop working. But, at the same time he didn’t want to pay the mason any more than one link in a day because he might run off and not return.

Cutting the chain was very difficult. What is the minimum number of cuts that the wealthy man could make in the chain and still pay the mason each day for seven days?

[from TestFunda vol. 1 (p. 1)]

Twisted Rope

Picture to yourself a length of rope, lying on a table in front of you. The cross section of the rope is a regular N sided polygon. Slide the ends of the rope towards you so that it almost forms a circle.

Now mentally grasp the ends of the rope in your hands. You are going to glue the ends of the rope together but before you do, twist your right wrist so that the polygonal end rotates through one nth of a full revolution. Repeat the twisting a total of T times, so that your mental wrist has rotated through T nths of a full revolution. NOW glue the ends together, so that the polygonal ends match with edges glued to edges.

When the mental glue has dried, start painting one facet (flat surface) of the rope and keep going until you find yourself painting over an already painted part. Begin again on another facet not yet painted, and use another colour.

How many colours do you need?

Bridge Crossing

Five persons are standing on one side of a bridge.
They want to cross the bridge.

Without a torch, they cannot proceed.
Only one torch is available.
The torch has a remaining battery life of only 30 seconds.

Only two people can go over the bridge at one time.
The torch needs to be returned to the remaining persons.

The five people take different times to cross the bridge.
One takes 1 second to cross the bridge.
The others take 3 seconds, 6 seconds, 8 seconds and 12 seconds.

Everyone crosses the bridge within 30 seconds.

How do they proceed?

Skyscrapers

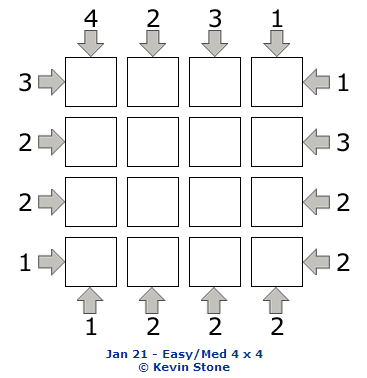
• You have to complete the grid such that every row and column contains the numbers 1 to 4.
• Each row and column contains each number only once.
• However, you have to follow the rules around the outside, which tell you how many skyscrapers you can see.
• You can’t see a shorter skyscraper behind a taller one.
• The puzzles can be quite hard and can require Sudoku techniques.

Locked Chest

In medieval times, the inhabitants of a remote village decided to lock the village valuables in a giant chest to protect them from marauding thieves. They placed a number of locks on the chest, with each lock needing its own distinct key. For additional security, the villagers made sure that any three people from the village would always have among them the keys needed to open the locks, but no two people would have the keys to do it.  

How many locks were required, and how many keys?