Salon Mathématique
Salon Mathématique started as a regularily scheduled gathering of teachers to explore issues around mathematics teaching and learning. The name is inspired by the salon’s of the 17th and 18th century where people met “under the roof of an inspiring host, held partly to amuse one another and partly to refine the taste and increase their knowledge of the participants through conversation” (Wikipedia – read more).
The Salon Mathématique meetings proved to be untenable. People were too busy to commit to a regular meeting schedule. As such, it is being moved to an online forum (still under construction).
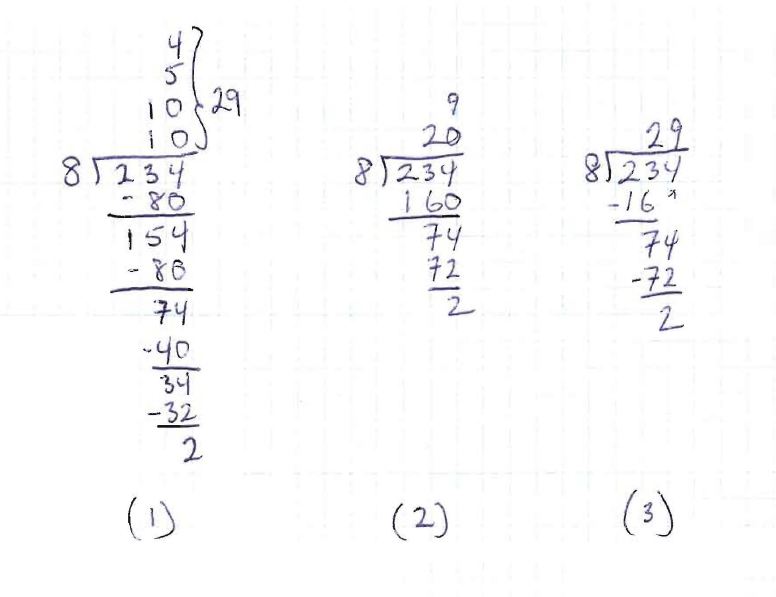
Salon Archive As always, we began the session by playing a number of games: Pentago, Pirate’s Gold, Pirate Hide and Seek, and GridWorks. The first and last of these have online versions. See Mathematical Thinking Games for links to these as well as other online games. This was followed by a wide ranging discussion on adapted vs. modified, French Immersion, and giftedness. It was truly a salon. Some of the specific things suggested were: January 25, 2011 – Division We started by playing around with two Smart Games – Camelot Jr. and Castle Logix. These are both award winning problem solving games that are a hit with kids big and small. We then moved directly into discussion on division touching briefly on the use of The Doorbell Rang as an excellent story book for introducing the concept. We explored the two types of division – partitive (also known as sharing or dealing) and quotitive (also known as measurement or scooping). Consider the problem 12 divided by 4. The partitive model would be divide 12 items into four groups and answer the question of how many in each group. That is, you are sharing 12 items among 4 groups. Alternatively, we can think of it as divide 12 items into groups of 4 and answer the question of how many groups. That is, you are scooping out 4’s and seeing how many times this can be done. The important thing here is that, although both models work for whole number division, only the quotitive model works for thinking about fraction division. For example, think about 2 divided by ½. If think of this as how many times can we scoop ½ out 2 we see that the answer is 4. Students come into kindergarten with the partitive (sharing) model already in place and it is important to make use of this in the early grades. But by grade 5 it is important that they start to explore division through the quotitive model as well so as to better set them up for success when they get to fractions. This was followed by a look at the alternate views of doing long division that focuses much more on the whole process as opposed to breaking it into parts. It also nicely emulates how groups of kids share large numbers of objects. This is sometimes referred to as the partial quotient algorithm. As can be seen below when the estimates are better it approaches the standard algorithm – but with more understanding. Meanwhile the secondary teachers explored factoring polynomials. Our conclusions were that: December 16, 2010 – Rational Numbers As usual, the meeting started with a game. In this case there were two award winning brain teaser games called Solitaire Chess and IQ Puzzler. After this we moved on to an activity wherein we did two explorations using the gears of a mountain bike. The first activity was about composite and prime numbers and had to do with calculating the number of gears on a bike. This is always the product of the number of chainrings and the number of sprockets in the cogset. We then followed this up by exploring rational numbers in terms of gear ratio. For a bicycle, the gear ratio for a give gear is the number of teeth on the chain ring divided by the number of teeth on the rear sprocket. This is also equivalent to the number of times the rear wheel will turn for one complete rotation of the crank for a given gear. So, for example, if the chainring has 42 teeth and the rear sprocket has 21 teeth then the gear ratio for that gear is 42/21 = 2. This means for one turn of the crank the rear wheel will turn twice. The activity that ensued was for the group to first calculate all the gear ratios for the mountain bike and then to put them in order. Such an activity, if used in the classroom, gives meaning to ratio, rational numbers, ordering of rational numbers, and the conversion between rational numbers and decimals. Individual conversations ensued with one particularly useful one having to do with sequencing activities for primary children. The suggestion was made to make an iconic clock with only an hour hand that shows (using diagrams) start of school, recess, lunch, end of school. Other regularly scheduled events can also be included, such as PE, Art, or daily physical activity. As for actual sequencing activities – many curriculum resources provide images that need to be put in order. I suggested that you make your own using a digital camera and photographing the children while doing an activity or through the day. Printing these images out and having them put them into order is now much more meaningful. November 16, 2010 – Placevalue We started the meeting by playing Chromino. Playing this game evolved into two separate problems: We then looked at a book called How to Live Dangerously by Warwick Cairnes which is an amusing look at how we as a society ignore statistics that should be relevant to our actions. The main part of the time together, however, was spent looking at two dilemma’ from the classroom. The first of these has to do with rounding numbers. Teachers find this seemingly simple concept difficult to teach. The main reason for this, I believe, is that students don’t see the point in this activity. So, I brought in some unusual rulers to deal with this. There was a ruler 100 cm long, one 10 cm long, and one 1 cm long. These were made out of old blinds and had one common characteristic – they were not graduated. That is, there were no markings on them. The idea is that if you give a child a 100 cm long ruler and ask them to measure the room then the idea of measuring it to the nearest 100 cm makes sense (as long as you tell them that estimation is not allowed). Similariy, if you give them the 100 cm long ruler and the 10 cm long ruler then they can measure to the nearest 10 cm – and so on. So, now rounding off becomes synonymous with accuracy – how accurate do you want the measurement to be? It also becomes clear that less accurate is quicker – which is sometimes the whole point of rounding. The activity can be changed by now calling the 100 cm ruler 10 dm or 1 m. The 10 cm ruler then becomes 1 dm or 0.1 m respectively. This allows us to move into the rounding of decimals. The second concept we dealt with was place value. Again, this seemingly intuitive concept is very challenging to teach. The reason for this is that there are really two concepts here. The first has to do with the concept of place value. This can be taught using popsicle sticks which are bundled into tens with rubber bands (and 10 bundles of ten are bundles into 100, and so on). This bundling and unbundling makes obvious the concepts of regrouping and decomposition which are conceptually more effective than carry and borrowing. The second concept has to do with magnitude of numbers represented in our base 10 system. which is so effective that it masks the true cardinality of our numbers. This is something that is often not understood until students grasp the concept of exponential growth in high school. But this need not be the case. First, there is no reason why the concept of exponential growth can’t be introduced in elementary school (as growing patterns) through things like the allowance problem (first week get a dollar – double every week thereafter) or the children’s book The Kings Chessboard. Although these are both examples of exponential growth where the numbers double it would be easy to extend them to tripling, quadrupling, all the way up to 10x. Even acting out the Kings Chessboard using rice would be VERY beneficial in helping them see the magnitudes of the numbers we deal with every day. Alternatively, there are a number of resources that can help students understand magnitude from the books How Much is a Million or One Million to web resources like How Much is a Million to the art work of Chris Jordan. October 19, 2010 – Feedback We started the meeting by playing a game of Guess Who. The game is an excellent example of how something simple can offer many pedagogical affordances. First, it is a game that relies on a strategy of trying, at each turn, to eliminate half of the remaining option. This is done by finding some attribute that is common to approximately half of the remaining game pieces. As such, it is an example of a binary search and, thus, can be used to model logarithmic and exponential growth. This game can be expanded in one of three ways: We then looked at the book How Many Elephants in a Blue Whale? and talked about it as a valuable resource for teaching non-standard units. This led to a brief discussion on If the World Was a Village as an example of how to scale large numbers and contexts into manageable and conceivable sizes. Finally, we did an activity around feedback and how different forms of feedback are appropriate or inappropriate for different contexts. We discussed feedback as serving a purpose – to affect change in the next iteration of student action – and how to use and facilitate the use of feedback effectively in the classroom. Salon discussions then ranged across a wide variety of topics: September 28, 2010 – Patterns The meeting started with a new game called Sumoku. We then moved onto an activity that had us exploring pattern activities from kindergarten up to grade 12. From these activities it became clear that there are really two very distinct forms of thinking required – with the grain and across the grain. As it turns out, while students have a propensity for the former of these, it is the later that is called upon more often as students progress through the grades. It also turns out that the curriculum is not well structured to allow students to develop their across the grain thinking. We then discussed how minor modifications to the curriculum as well as the introduction of matchstick problems could help with the development of this very important form of pattern thinking. A boy has $80 to buy 100 budgies. Blue budgies cost $3 each, green budgies cost $2 each, and yellow budgies cost $0.50 each. If he wants to ensure that he has at least one budgie of each colour and that he spends as much of his money as possible, how many of each colour does he need to buy?February 23, 2011 – Non-Mainstream Teaching
Resources
At this point the group split. The elementary teachers explored if it was possible to tell if it can be determined if a fraction will be a repeating decimal or not when the conversion is made. I won’t reveal the answer here, but I will say that the group did figure out that it has something to do with the prime factorization of the denominator.
Resources
Resources
Resources
Resources
Problem to Try (grades 4-12)
Resources
liljedahl | 
September 16, 2010 11:27 am